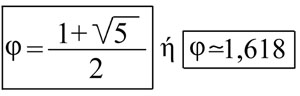
Ο Χρυσός Κανόνας

Ο Χρυσός Κανόνας, που αναπαριστάται με το ελληνικό γράμμα [φ], προς τιμή του γλύπτη Φειδία, είναι ένας αριθμός (ή ένας από τους αριθμούς) ο οποίος φαίνεται ότι πηγάζει από και σχετίζεται με τη βασική δομή του κόσμου μας. Ο χρυσός κανόνας εμφανίζεται πολύ συχνά σε καταστάσεις, αντικείμενα και διαδικασίες των οποίων η λειτουργία εξελίσσεται σε βήματα, αλλά όχι πάντα και απαραίτητα. Ο εν λόγω αριθμός έχει να κάνει και με την αρμονία, γι’ αυτό και συχνά συναντάται στην τέχνη ή στη γεωμετρία. Ένα παράδειγμα, για να κατανοήσουμε καλύτερα τη φύση του αριθμού, είναι η ακολουθία Fibonacci, όπου από έναν δοσμένο αριθμό, κάθε καινούργιος αριθμός αποτελεί το άθροισμα των δύο προηγούμενων. Ας πάρουμε μια βασική ακολουθία Fibonacci:

1-1-2-3-5-8-3-21-34-55-89-144…

Αν υπολογίσουμε το λόγο ανάμεσα σε οποιουσδήποτε δύο διαδοχικούς αριθμούς της ακολουθίας:
1/1 = 1
2/1 = 2
3/2 = 1.5
5/3 = 1.6666…
8/5 = 1.6
13/8 = 1.625
21/13 = 1.61538…
34/21 = 1.61904…
Συμπεραίνουμε ότι ο αριθμός στον οποίο τείνει να καταλήξει αυτός ο λόγος είναι το [φ]. Πάρτε για παράδειγμα το λόγο 34/21. Το πηλίκο διαφέρει από το [φ] μόνο κατά 0,001 περίπου.

Η Χρυσή Τομή

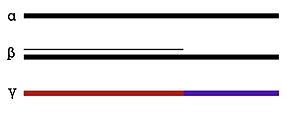
Πιθανόν να έχετε ακούσει τον όρο. Ας δούμε όμως τι ακριβώς είναι  η χρυσή τομή.
Ας πάρουμε μια ευθεία π.χ. 18 cm (α).
Αν κάνουμε τη διαίρεση: 18/φ έχουμε το μικρότερο ευθύγραμμο τμήμα που φαίνεται στην εικόνα (β).
Ο όρος “χρυσή τομή” αναφέρεται στην περίπτωση (γ), τη διαίρεση, δηλαδή, ενός ευθύγραμμου τμήματος σε αναλογίες του [φ].

Εφαρμογές στη Γεωμετρία

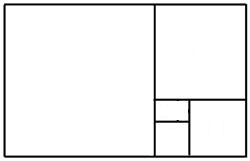
Αν πάρουμε ένα ορθογώνιο του οποίου οι πλευρές, αν διαιρεθούν, μας δίνουν τον αριθμό [φ] (για παράδειγμα, ένα ορθογώνιο με διαστάσεις 13 x 8), αυτό το ορθογώνιο ονομάζεται “χρυσό ορθογώνιο”. Αυτό έχει την εξής ενδιαφέρουσα ιδιότητα:
Αν σχεδιάσουμε ένα νέο ορθογώνιο με μήκος το άθροισμα των διαστάσεων του ορθογωνίου που έχουμε, το καινούργιο ορθογώνιο είναι και αυτό χρυσό. Στη συγκεκριμένη περίπτωση (13 x 8), το νέο ορθογώνιο έχει διαστάσεις (13 + 8 =)21 x 13. (Παρατηρήστε την εικόνα δίνοντας σημασία στα ορθογώνια και όχι στα τετράγωνα που φαίνονται).

Επίσης:
Αν ξεκινήσουμε με ένα τετράγωνο (1 x 1) και αρχίσουμε να περιστρέφουμε τις πλευρές για να φτιάξουμε ορθογώνια, όπως φαίνεται στην παρακάτω εικόνα:

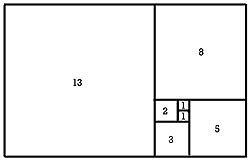
Καταλήγουμε σε χρυσά ορθογώνια, οι διαστάσεις των οποίων διαδοχικά είναι οι εξής:

1 x 1
2 x 1
3 x 2
5 x 3
8 x 5
13 x 8
21 x 13
34 x 21
…

Μήπως σας θυμίζει την ακολουθία Fibonacci;

Η αρχαία αρχιτεκτονική είναι γεμάτη από χρυσά ορθογώνια, και γενικά από αναλογίες του χρυσού κανόνα.

Ας δούμε ένα άλλο παράδειγμα, τη γνωστή σε όλους μας πεντάλφα, της οποίας η πρώτη ιστορική εμφάνιση ανάγεται στη Σχολή των Πυθαγορείων.

Έχουμε: ΑΔ/ΑΓ = φ, ΑΓ/ΑΒ = φ…   κτλ.

Μαθηματική ανάλυση

-Αριθμητική αναλογία έχουμε όταν σε μια ποσότητα προστεθεί μια άλλη ποσότητα.
-Γεωμετρική αναλογία έχουμε όταν μια ποσότητα πολλαπλασιαστεί με μία άλλη ποσότητα.

Με λίγα λόγια:

Αριθμητική αναλογία: πρόσθεση (+)
Γεωμετρική αναλογία: πολλαπλασιασμός (x)

Ο αριθμός [φ] παρουσιάζει και τις δύο ιδιότητες:

Έστω χρυσό ορθογώνιο με πλάτος 1 cm. Αφού το μήκος ενός χρυσού ορθογωνίου ισούται με το πλάτος του επί [φ], έχουμε:

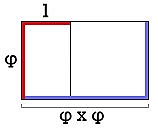
(Κόκκινο χρώμα: αρχικό ορθογώνιο – μπλε χρώμα: νέο ορθογώνιο)
Πλάτος: 1
Μήκος: 1 x φ = φ 
Ας φτιάξουμε τώρα ένα νέο χρυσό ορθογώνιο με πλάτος το μήκος του αρχικού:
Νέο πλάτος: φ
Είδαμε ήδη ότι στα χρυσά ορθογώνια το μήκος ισούται με το πλάτος επί [φ], άρα
Νέο μήκος: φ x φ
Αυτό αποτελεί μια γεωμετρική αναλογία.
Αλλά ξέρουμε ήδη ότι:
Νέο μήκος = μήκος αρχικού ορθογωνίου + πλάτος α.ο.
Νέο μήκος = φ + 1
Αυτό αποτελεί μια αριθμητική αναλογία.
Αφού αυτές οι δύο εκφράσεις περιγράφουν το ίδιο πράγμα είναι ισοδύναμες, άρα:

[φ] + 1 = [φ] x [φ] !

Ωραία…Τα είπαμε για τον χρυσό κανόνα. Και τι μ’ αυτό; Τι είναι τόσο σημαντικό σ’ αυτόν;
Κι όμως, εκτός από την τέχνη, τη γεωμετρία και άλλες ανθρώπινες ασχολίες, ο χρυσός κανόνας συναντάται πολύ συχνά και στη φύση.
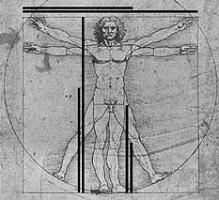
Για παράδειγμα, το ίδιο το ανθρώπινο σώμα είναι γεμάτο από αναλογίες του [φ].
Απλά προσέξτε τις παρακάτω εικόνες:

Άλλο παράδειγμα: Ένα από τα πιο γνωστά είδη κοχυλιού (Nautilus pompilius) μεγαλώνει σε κάθε σπείρα κατά [φ]:

Σύνοψη: Ο χρυσός κανόνας συναντάται πολύ συχνά στη φύση, αλλά επειδή παρουσιάζει εξαιρετική αρμονία καταφεύγουμε σ’ αυτόν σε πολλές περιπτώσεις. Σκεφτείτε, θα σας βόλευε η οθόνη μπροστά στην οποία κάθεστε αυτή τη στιγμή να είναι τετράγωνη;…